3D Mesh

images/download/attachments/122260024/Cmd3DMesh.svg

This command creates a 3D mesh from point cloud(s). You can mesh as many clouds as you want at the same time.

Requirements

Select all the points, polylines, and clouds to mesh and launch the command. All the vertices of these entities will be automatically extracted to create the mesh.

Point cloud property: displays information about the cloud. The number of points is the total of all the points inside your selection (several entities may be selected together).
Noise reduction: strategy to apply in order to reduce the noise.
1. Meshing in two steps: you create, in the first step, a rough mesh with regular triangles. You must enter the average distance between points for this first calculation step. The noise reduction will be more efficient if this distance is large. Then, another dialog box will be opened to refine the mesh with deviation error criteria.
2. Regular Sampling: the cloud is sampled to keep the least noisy points. You must enter the average distance between points. The noise reduction will be more efficient if this distance is large.
3. 3D deviation filtering: all the points are considered as having the same "weight" according to the noise. There is no sampling to reduce the noise. This option provides a faster calculation in case of "mathematically exact" points (for example coming from the sampling on a CAD model). The points are chosen to satisfy the deviation error criterion. You must enter the value to be used for the 3D deviation error (accuracy). A low value provides a better meshing of small details.
4. Regular Sampling + 3D deviation filtering: if possible, the least noisy points are used to create triangles according to the average distance between points. In the case where the 3D deviation error is not reached, other points could also be chosen.
5. Keep all the points: all the points are kept inside the mesh. This option is available only if your point cloud contains a small number of points (less than about 400 000). This option is automatically disabled if the number of points is too high.
Hole management: strategy to apply to fill or smooth holes.
1. Hole detection: Holes with a extension smaller than the entered triangle size will be closed by the algorithm. You should enter the maximum triangle size to fill the small and smooth the big holes.
2. Try to keep only the external border: If possible, try to create a polyhedron with an external border and without holes: all holes but the largest one will be filled.
3. Try to create a watertight mesh: if possible, try to create a polyhedron without any hole (closed).
By default, if the cloud contains scanning directions, they are used for the mesh computation, but you have the possibility to Ignore scanning directions.

Notes

When you launch the command, the software parses the selected object(s) to automatically determine the default parameters that will give a good result most often (number of points, size, noise, etc.). Then, if you simply click OK, the result is generally correct.
Do not enter a too small deviation value, otherwise, the calculation time will be long, the polyhedron will be heavy, and the result will be disappointing (aberrant points, noise, spiky result). With a zero value, all the points will be kept.

Technical information

From the mathematical point of view, the best accuracy is obtained by keeping all the points of your cloud inside the mesh. This means:

No noise reduction.
Zero deviation error.

Unfortunately this is purely mathematic and theoretical because, in reality, most point clouds contain measurement error so that some of the points are over the real surface while other points are below the real surface. If you make a mesh keeping all these points, you will obtain many undulations around the surface. Most often, you will obtain a disappointing result:

The number of triangles will increase dramatically, as well as the quantity of RAM memory that your model will require. If the number of triangles is really too high, you can get errors.
The size of the resulting file will be very big and probably difficult to process by other software.
The response time will become bad due to the number of triangles.
The surface state will be very bad. The undulation of the surface is often called "noise" by analogy of sound wave oscillations.

images/download/attachments/122260024/3DRAppShoe2.JPG

Meshing with a too small deviation error provides often a "noisy" surface (orange skin effect).

The goal is generally to create a mesh having the best quality possible. The quality is a compromise between:

Accuracy.
Level of detail.
Smoothness of the surface.
Number of triangles.

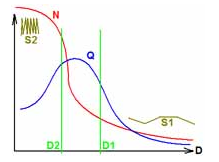
When the deviation error D decreases, the number of points N increases. A deviation error of zero means keep all points. If the deviation error is high, the level of detail is low and the surface is roughly defined (See S1 on the figure). If the deviation error is too small or zero the surface contains many spikes (See S2 on the figure). Between the two extreme values, the goal is to find the optimum value of the deviation error, which provides the optimum quality Q.

Depending on the quality of the original point cloud (noisy and aberrant points, missing parts, ...), it is often useful to mesh first using a big noise reduction parameter (and then refine one or several times), rather than directly creating a very accurate mesh with a small noise reduction.

images/download/attachments/122260024/image2015-12-10_11_6_9.png

When the deviation error D decreases the number of points N increases. The quality optimum Q is reached between D1 and D2