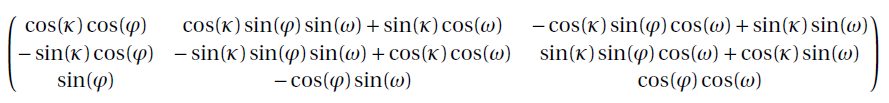Edit Image
This function allows you to modify the internal and external parameters of an image.
Select one or several images before entering the command.
Note
While it is possible to select several images before entering the command, only their image type and their internal parameters will be editable. The edited parameters will be applied to all the selected images.
Editing several images using different projections methods at the same time is not possible.
The content of the command will vary according to the image type.
|
|
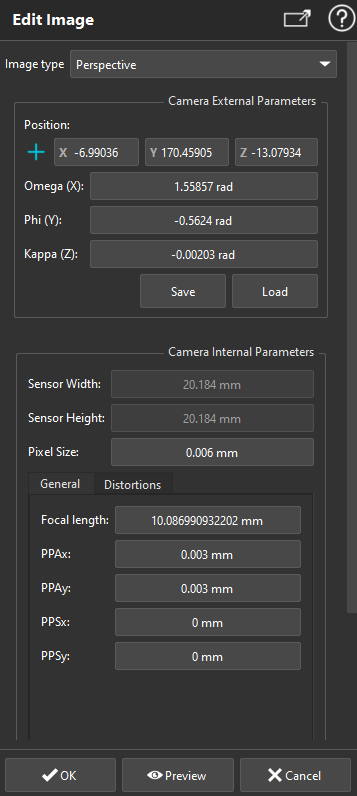
Perspective image
Note Perspective projection modelClassical perspective projection using a standard pinhole camera model coupled with lens radial and tangential distortions are expressed as follows: Knowing a 3D Point P located at the coordinates [X Y Z] in the world coordinate system, the first step is to compute the point P coordinates in the camera coordinate system. This point P in the camera coordinates system can be expressed as P' of coordinates [X' Y' Z'] such as P' = R P + t. With R the rotation matrix and t the camera position in the world coordinates as expressed in the camera external parameters. The homogeneous coordinates of the point P' are computed to obtain the point p = [X' / Z' Y' / Z' Z' / Z'] = [x y 1] This point p is then shifted according to the principal point of symmetry (PPS [xp yp]) location such as x' = x - xp and y' = y-yp Using these centered coordinates the computation of the distortions is possible. Radial distortion: Δxr = x' (1.0 - k0 + k1r2 + k 2 r4 + k3r6 + k4r8 + k5r10 + k6r12) Δyr = y' (1.0 - k0 + k1r2 + k2r4 + k3r6 + k4r8 + k5r10 + k6r12) Tangential distortion: Δxd = p1 (r2 + 2x'2) + 2 p2 x' y'
Δyd = p2 (r2 + 2y'2) + 2 p1 x' y' The distorted point coordinates are simply: xc = Δxr + Δxd yc = Δyr + Δyd From these distorted coordinates, the final UV coordinates are obtained as: U = f xc + ( PPA x / SW ) V = f yc + ( PPAy / SH ) |
|
|
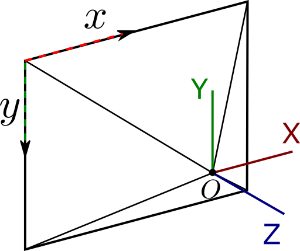
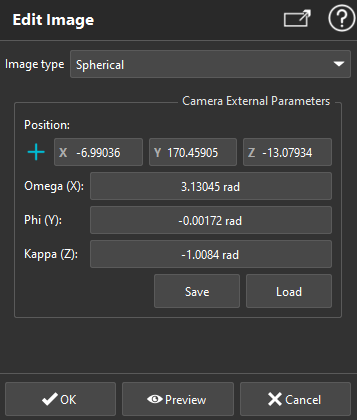
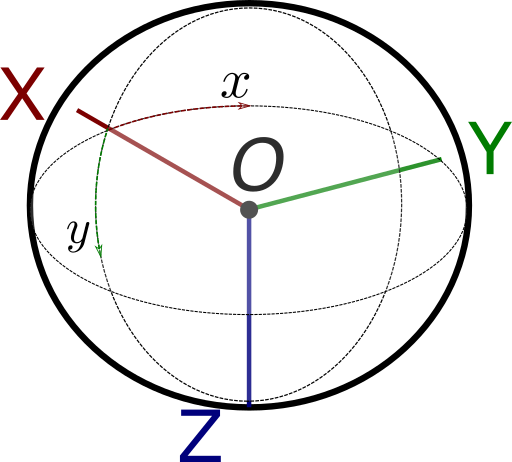
Spherical ImageImage type dropdown menu allows you to manually change the projection type of the image. Warning Modifying the image type may result in the loss of one or several internal parameters. Camera External Parameters let you modify the pose (position and orientation) of the selected image. Note Images rotation and standards (Spherical)The original pose of a spherical image (without any translation or rotation) is the following. The spherical image center is located on the scene origin, the center of the spherical image is corresponds to the X axis, the top direction of the image is given by the -Z axis and the right direction of the image given by the Y axis.
Photogrammetry angles (ω φ κ)The main image orientation process consists in providing for each image to texture, three photogrammetric angles that will define the image orientation in the scene. The supported rotation convention is the Standard Omega Phi Kappa (Euler Angles) In this rotation configuration the rotation are performed in the Order X => Y => Z. The rotations values are given by omega, phi and kappa Ox(ω), Oy(φ), Oz(κ). The rotation matrix corresponding to this rotation is computed as follows:
|
|
|
Orthoimage
Warning Modifying the image type may result in the loss of one or several internal parameters.
|